Quasi tutti i nostri modelli scientifici convenzionali sono pieni di inconsistenze e nei mass media non se ne discute mai... La scienza ufficiale non sa cosa sia la materia veramente...
L'UNIVERSO E DA SEMPRE REGOLATO E GESTITO DA FORZE ED ENERGIE SCONOSCIUTE MA BEN REALI E PRESENTI IN UN CONTESTO ARMONICO E GEOMETRICO. OVE LA MATERIA E L'ANTIMATERIA SONO INCONTRASTATE DOMINATRICI UNICHE DELL'UNIVERSO E DELLO SPAZIO ASSOLUTO CHE AD ESSO NE E' INTERCONNESSO.
Fibonacci e il rettangolo aureo!!!!
Un processo di formazione e rottura di simmetria possono formare una base di matematica per l'evoluzione della vita. (teoria)
Sezione aurea.
Il matematico pisano
Leonardo Fibonacci (1175), ricordato soprattutto per via della sua
sequenza divenuta ormai celeberrima, fece parte della cerchia dei dotti
che gravitava attorno alla corte di Federico II di Svevia. Durante i
suoi numerosi viaggi, dopo avere assimilato le conoscenze matematiche
del mondo arabo, pubblicò intorno al 1202 il “Liber  Abaci”,
con cui si propose di diffondere nel mondo scientifico occidentale le
regole di calcolo note agli Arabi, ovvero il sistema decimale ad oggi in
uso in Europa. Un problema esposto nel Liber Abaci riguarda sette
vecchie che andavano a Roma, ognuna con sette muli, ogni mulo carico di
sette sacchi, ogni sacco contenente sette pani, per ogni pane sette
coltelli, ogni coltello in sette foderi. Ci si domanda quanti oggetti
sono stati trasportati globalmente e l'autore fornisce la risposta
applicando il concetto della serie geometrica con valore iniziale 7 e
ragione 7, i cui 6 termini devono essere sommati e come totale si
ottiene 137.256 oggetti (comprese le 7 vecchie). La successione di
questi numeri è chiamata successione di Fibonacci. Fibonacci fu il primo
algebrista cristiano, il più grande matematico del medioevo, il maggior
genio scientifico del XIII secolo in Italia; è del 1220 il De practica
geometriae, nel quale applicò il nuovo sistema aritmetico alla
risoluzione di problemi geometrici, un trattato di geometria e
trigonometria. Il decreto della Repubblica di Pisa gli conferì il titolo
di Discretus et sapiens magister Leonardo Bigollo, a riconoscimento dei
grandi progressi che apportò alla matematica. Fibonacci morì qualche
tempo dopo il 1240, presumibilmente a Pisa. La sequenza di Fibonacci si
compone di una serie di numeri (0,1,1,2,3,5,8,13,21,34,55,89,144...) e
presenta interessanti proprietà:
Abaci”,
con cui si propose di diffondere nel mondo scientifico occidentale le
regole di calcolo note agli Arabi, ovvero il sistema decimale ad oggi in
uso in Europa. Un problema esposto nel Liber Abaci riguarda sette
vecchie che andavano a Roma, ognuna con sette muli, ogni mulo carico di
sette sacchi, ogni sacco contenente sette pani, per ogni pane sette
coltelli, ogni coltello in sette foderi. Ci si domanda quanti oggetti
sono stati trasportati globalmente e l'autore fornisce la risposta
applicando il concetto della serie geometrica con valore iniziale 7 e
ragione 7, i cui 6 termini devono essere sommati e come totale si
ottiene 137.256 oggetti (comprese le 7 vecchie). La successione di
questi numeri è chiamata successione di Fibonacci. Fibonacci fu il primo
algebrista cristiano, il più grande matematico del medioevo, il maggior
genio scientifico del XIII secolo in Italia; è del 1220 il De practica
geometriae, nel quale applicò il nuovo sistema aritmetico alla
risoluzione di problemi geometrici, un trattato di geometria e
trigonometria. Il decreto della Repubblica di Pisa gli conferì il titolo
di Discretus et sapiens magister Leonardo Bigollo, a riconoscimento dei
grandi progressi che apportò alla matematica. Fibonacci morì qualche
tempo dopo il 1240, presumibilmente a Pisa. La sequenza di Fibonacci si
compone di una serie di numeri (0,1,1,2,3,5,8,13,21,34,55,89,144...) e
presenta interessanti proprietà:
 La somma di due numeri contigui forma il successivo numero della sequenza (es. 3+5=8; 13+21=34; 55+89=144; ecc...);
La somma di due numeri contigui forma il successivo numero della sequenza (es. 3+5=8; 13+21=34; 55+89=144; ecc...);
 Il rapporto tra due termini successivi si avvicina molto rapidamente a 0,618;
Il rapporto tra due termini successivi si avvicina molto rapidamente a 0,618;
 Il
rapporto fra un numero e il suo precedente tende a 1,618. Questo
numero, indicato dalla lettera greca PHI, è detto rapporto aureo: è un
numero irrazionale con molte curiose e misteriose proprietà...;
Il
rapporto fra un numero e il suo precedente tende a 1,618. Questo
numero, indicato dalla lettera greca PHI, è detto rapporto aureo: è un
numero irrazionale con molte curiose e misteriose proprietà...;
 Il rapporto di un numero per il secondo che lo precede è sempre pari (tendente a) 2,618, che è il quadrato di 1,618;
Il rapporto di un numero per il secondo che lo precede è sempre pari (tendente a) 2,618, che è il quadrato di 1,618;
 Il quadrato di qualsiasi numero della serie è uguale al numero che lo
precede, per il numero che lo segue, più o meno 1. Il più o meno si
alterna lungo la sequenza;
Il quadrato di qualsiasi numero della serie è uguale al numero che lo
precede, per il numero che lo segue, più o meno 1. Il più o meno si
alterna lungo la sequenza;
 Se
dividiamo qualsiasi numero per il secondo che lo precede nella
sequenza, otterremo sempre due come risultato, e come resto il numero
immediatamente precedente il divisore. Per esempio: 8934=2 con il resto
di 21;
Se
dividiamo qualsiasi numero per il secondo che lo precede nella
sequenza, otterremo sempre due come risultato, e come resto il numero
immediatamente precedente il divisore. Per esempio: 8934=2 con il resto
di 21;
 Il quadrato di un numero di Fibonacci meno il quadrato del secondo numero precedente è sempre un numero della successione;
Il quadrato di un numero di Fibonacci meno il quadrato del secondo numero precedente è sempre un numero della successione;
 Il massimo comun divisore di due numeri di Fibonacci è ancora un numero di Fibonacci;
Il massimo comun divisore di due numeri di Fibonacci è ancora un numero di Fibonacci;
 Escludendo
1 e 2, ogni numero della serie, moltiplicato per 4, fornisce un
risultato, che aggiunto ad un numero di una nuova serie, dà un'altra
serie di Fibonacci.
Escludendo
1 e 2, ogni numero della serie, moltiplicato per 4, fornisce un
risultato, che aggiunto ad un numero di una nuova serie, dà un'altra
serie di Fibonacci.
Esempio: 3x4=12+1=13; 5x4=20+1=21; 8x4=32+2=34; 13x4=52+3=55; 21x4=84+5=89 e così via…
 Abaci”,
con cui si propose di diffondere nel mondo scientifico occidentale le
regole di calcolo note agli Arabi, ovvero il sistema decimale ad oggi in
uso in Europa. Un problema esposto nel Liber Abaci riguarda sette
vecchie che andavano a Roma, ognuna con sette muli, ogni mulo carico di
sette sacchi, ogni sacco contenente sette pani, per ogni pane sette
coltelli, ogni coltello in sette foderi. Ci si domanda quanti oggetti
sono stati trasportati globalmente e l'autore fornisce la risposta
applicando il concetto della serie geometrica con valore iniziale 7 e
ragione 7, i cui 6 termini devono essere sommati e come totale si
ottiene 137.256 oggetti (comprese le 7 vecchie). La successione di
questi numeri è chiamata successione di Fibonacci. Fibonacci fu il primo
algebrista cristiano, il più grande matematico del medioevo, il maggior
genio scientifico del XIII secolo in Italia; è del 1220 il De practica
geometriae, nel quale applicò il nuovo sistema aritmetico alla
risoluzione di problemi geometrici, un trattato di geometria e
trigonometria. Il decreto della Repubblica di Pisa gli conferì il titolo
di Discretus et sapiens magister Leonardo Bigollo, a riconoscimento dei
grandi progressi che apportò alla matematica. Fibonacci morì qualche
tempo dopo il 1240, presumibilmente a Pisa. La sequenza di Fibonacci si
compone di una serie di numeri (0,1,1,2,3,5,8,13,21,34,55,89,144...) e
presenta interessanti proprietà:
Abaci”,
con cui si propose di diffondere nel mondo scientifico occidentale le
regole di calcolo note agli Arabi, ovvero il sistema decimale ad oggi in
uso in Europa. Un problema esposto nel Liber Abaci riguarda sette
vecchie che andavano a Roma, ognuna con sette muli, ogni mulo carico di
sette sacchi, ogni sacco contenente sette pani, per ogni pane sette
coltelli, ogni coltello in sette foderi. Ci si domanda quanti oggetti
sono stati trasportati globalmente e l'autore fornisce la risposta
applicando il concetto della serie geometrica con valore iniziale 7 e
ragione 7, i cui 6 termini devono essere sommati e come totale si
ottiene 137.256 oggetti (comprese le 7 vecchie). La successione di
questi numeri è chiamata successione di Fibonacci. Fibonacci fu il primo
algebrista cristiano, il più grande matematico del medioevo, il maggior
genio scientifico del XIII secolo in Italia; è del 1220 il De practica
geometriae, nel quale applicò il nuovo sistema aritmetico alla
risoluzione di problemi geometrici, un trattato di geometria e
trigonometria. Il decreto della Repubblica di Pisa gli conferì il titolo
di Discretus et sapiens magister Leonardo Bigollo, a riconoscimento dei
grandi progressi che apportò alla matematica. Fibonacci morì qualche
tempo dopo il 1240, presumibilmente a Pisa. La sequenza di Fibonacci si
compone di una serie di numeri (0,1,1,2,3,5,8,13,21,34,55,89,144...) e
presenta interessanti proprietà:Esempio: 3x4=12+1=13; 5x4=20+1=21; 8x4=32+2=34; 13x4=52+3=55; 21x4=84+5=89 e così via…
Dato
un segmento AC, si fissi un punto intermedio B in modo che lo divida in
parti diseguali, le parti sono dette in rapporto aureo quando il tratto
più corto BC sta al tratto più lungo AB come il tratto più lungo AB sta
al segmento intero AC.

La proporzione è così espressa:
Per
avere l'idea della proporzione, supponiamo che il segmento sia pari ad
1, possiamo così calcolare la misura dei due tratti AB e BC:
uguagliando i termini e ricordando che AC = 1, si ottiene
il rapporto tra i due segmenti è pari a:
Consideriamo
un rettangolo con i lati in rapporto aureo AD/AB = 1,618. Se al suo
interno tracciamo un quadrato, il rettangolo minore restante avrà i lati
in rapporto aureo AB/AE = 1,618.
 |
 |
Se
ripetiamo questa operazione un numero infinito di volte, otterremo
sempre dei rettangoli con i lati in rapporto aureo tra loro...
Dato
un pentagono regolare ABCDE con lati uguali ed angoli uguali, tracciamo
una diagonale BE che unisca due vertici qualsiasi del pentagono. Se
dividiamo la lunghezza della diagonale  BE
per la lunghezza di un lato AB, otterremo il valore 1,618 ! Se
tracciamo ora una seconda diagonale AD all’interno del pentagono, ogni
diagonale sarà divisa in due parti: il rapporto tra le due parti e tra
la parte maggiore e
BE
per la lunghezza di un lato AB, otterremo il valore 1,618 ! Se
tracciamo ora una seconda diagonale AD all’interno del pentagono, ogni
diagonale sarà divisa in due parti: il rapporto tra le due parti e tra
la parte maggiore e l'intera diagonale sarà pari a PHI = 1,618. Se tracciamo tutte le
diagonali del pentagono, esse formeranno una stella a cinque punte o
pentangolo al cui interno apparirà un pentagono invertito che sarà in
rapporto aureo PHI con il primo pentagono... Il pentagono stellato è
l'intera diagonale sarà pari a PHI = 1,618. Se tracciamo tutte le
diagonali del pentagono, esse formeranno una stella a cinque punte o
pentangolo al cui interno apparirà un pentagono invertito che sarà in
rapporto aureo PHI con il primo pentagono... Il pentagono stellato è  sicuramente
la figura geometrica che più di ogni altra rappresenta, all'infinito,
la sezione aurea. E' forse per questo motivo che questo fu scelto come
simbolo della scuola pitagorica; a questa figura è stata attribuita per
millenni un’importanza misteriosa probabilmente per la sua proprietà di
generare la sezione aurea , da cui è nata.
sicuramente
la figura geometrica che più di ogni altra rappresenta, all'infinito,
la sezione aurea. E' forse per questo motivo che questo fu scelto come
simbolo della scuola pitagorica; a questa figura è stata attribuita per
millenni un’importanza misteriosa probabilmente per la sua proprietà di
generare la sezione aurea , da cui è nata.
 BE
per la lunghezza di un lato AB, otterremo il valore 1,618 ! Se
tracciamo ora una seconda diagonale AD all’interno del pentagono, ogni
diagonale sarà divisa in due parti: il rapporto tra le due parti e tra
la parte maggiore e
BE
per la lunghezza di un lato AB, otterremo il valore 1,618 ! Se
tracciamo ora una seconda diagonale AD all’interno del pentagono, ogni
diagonale sarà divisa in due parti: il rapporto tra le due parti e tra
la parte maggiore e l'intera diagonale sarà pari a PHI = 1,618. Se tracciamo tutte le
diagonali del pentagono, esse formeranno una stella a cinque punte o
pentangolo al cui interno apparirà un pentagono invertito che sarà in
rapporto aureo PHI con il primo pentagono... Il pentagono stellato è
l'intera diagonale sarà pari a PHI = 1,618. Se tracciamo tutte le
diagonali del pentagono, esse formeranno una stella a cinque punte o
pentangolo al cui interno apparirà un pentagono invertito che sarà in
rapporto aureo PHI con il primo pentagono... Il pentagono stellato è  sicuramente
la figura geometrica che più di ogni altra rappresenta, all'infinito,
la sezione aurea. E' forse per questo motivo che questo fu scelto come
simbolo della scuola pitagorica; a questa figura è stata attribuita per
millenni un’importanza misteriosa probabilmente per la sua proprietà di
generare la sezione aurea , da cui è nata.
sicuramente
la figura geometrica che più di ogni altra rappresenta, all'infinito,
la sezione aurea. E' forse per questo motivo che questo fu scelto come
simbolo della scuola pitagorica; a questa figura è stata attribuita per
millenni un’importanza misteriosa probabilmente per la sua proprietà di
generare la sezione aurea , da cui è nata.
Se all’interno di un rettangolo aureo si disegna un quadrato con lato uguale al lato minore del  rettangolo,
il rettangolo differenza sarà anch’esso un rettangolo aureo.
L'operazione andrà ripetuta più di volte al fine di ottenere un effetto
visivo adeguato. Puntiamo il compasso sul vertice del quadrato che giace
sul lato lungo del rettangolo e tracciamo l’arco che unisce gli
estremi dei due lati che formano l'angolo scelto. Ripetiamo l'operazione
per ogni quadrato disegnato in modo da creare una linea continua,
otterremo così la spirale aurea.
rettangolo,
il rettangolo differenza sarà anch’esso un rettangolo aureo.
L'operazione andrà ripetuta più di volte al fine di ottenere un effetto
visivo adeguato. Puntiamo il compasso sul vertice del quadrato che giace
sul lato lungo del rettangolo e tracciamo l’arco che unisce gli
estremi dei due lati che formano l'angolo scelto. Ripetiamo l'operazione
per ogni quadrato disegnato in modo da creare una linea continua,
otterremo così la spirale aurea.
Sin
dai tempi più antichi esiste una proporzione divina (o sezione aurea)
che è stata presa in considerazione per ottenere una dimensione armonica
delle cose. Dalla geometria all'architettura, dalla pittura alla musica
possiamo osservare come tale rappresentazione corrisponda ad un
rapporto che è stato definito pari a 1.618. Gli esempi in natura di
elementi che richiamano la serie di Fibonacci sono numerosissimi.Tra i
primi utilizzatori di questo rapporto ci furono sicuramente i Greci. Il
rapporto tra lunghezza e larghezza nei templi rettangolo,
il rettangolo differenza sarà anch’esso un rettangolo aureo.
L'operazione andrà ripetuta più di volte al fine di ottenere un effetto
visivo adeguato. Puntiamo il compasso sul vertice del quadrato che giace
sul lato lungo del rettangolo e tracciamo l’arco che unisce gli
estremi dei due lati che formano l'angolo scelto. Ripetiamo l'operazione
per ogni quadrato disegnato in modo da creare una linea continua,
otterremo così la spirale aurea.
rettangolo,
il rettangolo differenza sarà anch’esso un rettangolo aureo.
L'operazione andrà ripetuta più di volte al fine di ottenere un effetto
visivo adeguato. Puntiamo il compasso sul vertice del quadrato che giace
sul lato lungo del rettangolo e tracciamo l’arco che unisce gli
estremi dei due lati che formano l'angolo scelto. Ripetiamo l'operazione
per ogni quadrato disegnato in modo da creare una linea continua,
otterremo così la spirale aurea. greci era di preferenza 1,618. La pianta del Partenone di Atene, ad
esempio, è un rettangolo con lati di dimensioni tali che la lunghezza è
pari alla radice di 5 volte la larghezza, mentre nell'architrave in
facciata il rettangolo aureo è ripetuto più volte. In un'anfora greca
(IV secolo a.C.) il diametro maggiore sta al diametro del collo come 1 :
0,618; il listello all'altezza dei manici divide l'altezza totale in
una proporzione aurea che si riduce anche nel rapporto tra la fascia
decorata a figure e la parte superiore del vaso.
greci era di preferenza 1,618. La pianta del Partenone di Atene, ad
esempio, è un rettangolo con lati di dimensioni tali che la lunghezza è
pari alla radice di 5 volte la larghezza, mentre nell'architrave in
facciata il rettangolo aureo è ripetuto più volte. In un'anfora greca
(IV secolo a.C.) il diametro maggiore sta al diametro del collo come 1 :
0,618; il listello all'altezza dei manici divide l'altezza totale in
una proporzione aurea che si riduce anche nel rapporto tra la fascia
decorata a figure e la parte superiore del vaso.Percorrendo il lungo pendio che conduce all’altopiano di Giza, nei pressi del Cairo, pare di
 scorgere
in lontananza tre montagne dai contorni particolarmente nitidi. Man
mano che ci avviciniamo, però, riconosciamo quelle gigantesche forme per
quello che sono: piramidi. Ed una volta giunti a ridosso, la loro mole è
ancora più impressionante. Lo
scorgere
in lontananza tre montagne dai contorni particolarmente nitidi. Man
mano che ci avviciniamo, però, riconosciamo quelle gigantesche forme per
quello che sono: piramidi. Ed una volta giunti a ridosso, la loro mole è
ancora più impressionante. Lo  spazio
visivo è occupato per metà dalla pietra e per metà dal cielo. La più
alta è la Grande Piramide di Cheope. La centrale appartiene a Chefren ed
è solo leggermente più piccola, mentre la più bassa è la tomba di
Micerino. La piramide egizia di Cheope, costruita molti secoli prima del
Partenone, ha una base di 230 metri ed una altezza di 145: il rapporto
base/altezza corrisponde a 1,58, molto vicino a 1,618.
spazio
visivo è occupato per metà dalla pietra e per metà dal cielo. La più
alta è la Grande Piramide di Cheope. La centrale appartiene a Chefren ed
è solo leggermente più piccola, mentre la più bassa è la tomba di
Micerino. La piramide egizia di Cheope, costruita molti secoli prima del
Partenone, ha una base di 230 metri ed una altezza di 145: il rapporto
base/altezza corrisponde a 1,58, molto vicino a 1,618.In una della prime opere dedicate a Re Artù, la Vita Merlini (circa 1140) di Geoffrey di Monmouth, si parla di un complesso circolare, composto da enormi pietre, la Chorea Gigantum (Danza dei giganti), che si trovava in Africa, poi era stato portato in Irlanda da un
 popolo di giganti. Qui era stato sistemato sul Monte Killarus, come
monumento funebre per quattrocentosessanta nobili soldati di Aurelio
Ambrosius uccisi dai Sassoni. Re Uther Pendragon tentò di trasportarlo
in Inghilterra, ma l'impresa era superiore alle sue forze, così dovette
rivolgersi al mago Merlino. Questi, con l'aiuto degli angeli, lo
trasferì nella piana di Salisbury, dove esiste tuttora con il nome di
Stonehenge. Nei megaliti di Stonehenge, le superfici teoriche dei due
cerchi di pietre azzurre e di Sarsen, stanno tra loro nel rapporto di
1,618
popolo di giganti. Qui era stato sistemato sul Monte Killarus, come
monumento funebre per quattrocentosessanta nobili soldati di Aurelio
Ambrosius uccisi dai Sassoni. Re Uther Pendragon tentò di trasportarlo
in Inghilterra, ma l'impresa era superiore alle sue forze, così dovette
rivolgersi al mago Merlino. Questi, con l'aiuto degli angeli, lo
trasferì nella piana di Salisbury, dove esiste tuttora con il nome di
Stonehenge. Nei megaliti di Stonehenge, le superfici teoriche dei due
cerchi di pietre azzurre e di Sarsen, stanno tra loro nel rapporto di
1,618Nelle arti del passato, in molte opere di Leonardo da Vinci, Piero della Francesca, Bernardino Luini, Sandro Botticelli, si ricorreva spesso alla sezione aurea (la divina proportione), considerata quasi la chiave mistica dell'armonia nelle arti e nelle scienze. Beethoven, nelle “33 variazioni sopra un valzer di Dabelli”, suddivise la sua composizione in parti corrispondenti corrispondenti ai numeri di Fibonacci.
La successione di Fibonacci è onnipresente in natura.. Se moltiplichiamo per 1,618 la distanza che in una persona adulta va dai piedi all'ombelico, otteniamo la sua statura. Così la distanza dal gomito alla mano (con le dita tese) moltiplicata per 1,618, da la lunghezza totale del braccio. La distanza che va dal ginocchio all'anca moltiplicata per 1,618, dà la lunghezza della gamba, dall'anca al malleolo. Anche nella mano i rapporti tra le falangi delle dita medio e anulare sono aurei, così il volto umano è tutto scomponibile in una griglia i cui rettangoli hanno i lati in rapporto aureo.
Quasi tutti i fiori hanno tre, cinque, otto, tredici, ventuno, trentaquattro,
 cinquantacinque o
cinquantacinque o  ottantanove
petali: i gigli ne hanno tre, i ranuncoli cinque, il delphinium
spessone ne ha otto, la calendula tredici, l'astro ventuno e le
margherite di solito ne hanno trentaquattro, cinquantacinque o
ottantanove.
ottantanove
petali: i gigli ne hanno tre, i ranuncoli cinque, il delphinium
spessone ne ha otto, la calendula tredici, l'astro ventuno e le
margherite di solito ne hanno trentaquattro, cinquantacinque o
ottantanove.Troviamo i numeri di Fibonacci anche nei fiori di girasole. Le piccole infiorescenze al centro
 di
girasole, che poi si trasformano in semi, sono disposte lungo due
insiemi di spirali che girano rispettivamente in senso orario e
antiorario. Spesso le spirali orientate in senso orario sono
trentaquattro e quelle orientate in senso antiorario cinquantacinque; ma
a volta sono rispettivamente cinquantacinque e ottantanove, o
addirittura ottantanove e centoquarantaquattro, e si tratta sempre di
numeri di Fibonacci consecutivi (il cui rapporto si approssima alla
sezione aurea)
di
girasole, che poi si trasformano in semi, sono disposte lungo due
insiemi di spirali che girano rispettivamente in senso orario e
antiorario. Spesso le spirali orientate in senso orario sono
trentaquattro e quelle orientate in senso antiorario cinquantacinque; ma
a volta sono rispettivamente cinquantacinque e ottantanove, o
addirittura ottantanove e centoquarantaquattro, e si tratta sempre di
numeri di Fibonacci consecutivi (il cui rapporto si approssima alla
sezione aurea) Diversi
tipi di conchiglie (ad esempio quella del Nautilus) hanno una formaa
spirale fatta secondo i numeri di Fibonacci. In botanica, la
disposizione a frattali degli elementi che compongono le foglie degli
alberi, seguono un diagramma logaritmico analogo ai suoni emessi da un
monocordo.
Diversi
tipi di conchiglie (ad esempio quella del Nautilus) hanno una formaa
spirale fatta secondo i numeri di Fibonacci. In botanica, la
disposizione a frattali degli elementi che compongono le foglie degli
alberi, seguono un diagramma logaritmico analogo ai suoni emessi da un
monocordo.L'albero genealogico di un fuco presenta chiaramente la sequenza di Fibonacci. In uno sciame le api non sono tutte uguali: ci sono le api (femmine) e i fuchi (maschi). Le femmine
 sono
tutte generate dall’unione dell’ape regina con un fuco e si dividono in
operaie e regine. Le api regine sono api operaie nutrite con pappa
reale ma, diversamente dalle operaie, sono in grado di produrre uova. I
maschi nascono dalle uova dell ape regina. Le femmine hanno 2 genitori:
l’ape regina e un fuco, mentre i fuchi hanno un solo genitore, l’ape
regina. Se prendiamo in esame’l' albero genealogico di un fuco. 1 fuco
ha 1 genitore che a sua volta ha 2 genitori che a loro volta hanno 3
genitori che a loro volta hanno 5 genitori e così via.
sono
tutte generate dall’unione dell’ape regina con un fuco e si dividono in
operaie e regine. Le api regine sono api operaie nutrite con pappa
reale ma, diversamente dalle operaie, sono in grado di produrre uova. I
maschi nascono dalle uova dell ape regina. Le femmine hanno 2 genitori:
l’ape regina e un fuco, mentre i fuchi hanno un solo genitore, l’ape
regina. Se prendiamo in esame’l' albero genealogico di un fuco. 1 fuco
ha 1 genitore che a sua volta ha 2 genitori che a loro volta hanno 3
genitori che a loro volta hanno 5 genitori e così via.In condizioni ideali una coppia di conigli è in grado di riprodursi già un mese dopo la nascita. La femmina è in grado di generare una seconda coppia di conigli già un mese dopo l’accoppiamento con il maschio. Prendiamo una coppia di conigli e mettiamola in un recinto. Supponiamo che i nostri conigli non muoiano mai. Come si vede dal grafico all’inizio dell
 ’esperimento
abbiamo 1 coppia di conigli. Dopo un mese rimaniamo sempre con 1 coppia
di conigli. Dopo 2 mesi la femmina ha generato un’altra coppia di
conigli, quindi nel recinto abbiamo 2 coppie. Al terzo mese la prima
coppia ne ha generata un’altra, mentre la seconda non è stata in grado
di procreare, quindi nel recinto ci sono 3 coppie di conigli. Dopo un
altro mese, le prime due coppie generano altre due coppie mentre la
terza non procrea, quindi nel recinto ci sono 5 coppie di conigli e cosi
via di mese in mese...Questo esperimento assume come ipotesi che i
conigli non muoiano e che generino solo un altro paio di conigli alla
volta.
’esperimento
abbiamo 1 coppia di conigli. Dopo un mese rimaniamo sempre con 1 coppia
di conigli. Dopo 2 mesi la femmina ha generato un’altra coppia di
conigli, quindi nel recinto abbiamo 2 coppie. Al terzo mese la prima
coppia ne ha generata un’altra, mentre la seconda non è stata in grado
di procreare, quindi nel recinto ci sono 3 coppie di conigli. Dopo un
altro mese, le prime due coppie generano altre due coppie mentre la
terza non procrea, quindi nel recinto ci sono 5 coppie di conigli e cosi
via di mese in mese...Questo esperimento assume come ipotesi che i
conigli non muoiano e che generino solo un altro paio di conigli alla
volta. 
Negli oggetti quotidiani possiamo trovare alcuni esempi di sezione aurea, dalle schede telefoniche alle carte di credito e bancomat, dalle carte SIM dei cellulari alle musicassette: sono tutti rettangoli aurei con un rapporto tra base ed altezza pari a 1,618.
Tutti i pianeti interni distano dal Sole nelle proporzioni della successione di Fibonacci (Sole 1, Mercurio 1, Venere 2, Terra 3, Marte 5) e quelli esterni distano ugualmente da Giove (Giove 1, Saturno 1, Urano 2, Nettuno 3, Plutone 5); la distanza fra Marte e Giove è pari ad un decimo di quella fra il Sole e l' ultimo corpo astrale del Sistema Solare, cioè Plutone...
La magia dei frattali...
Frattale dell'insieme di Mandelbort
Frattali nella natura.
Le spirali sono alla base del mondo vivente. Il nucleo cellulare è costituito da una lunga catena a spirale, il DNA, riportante l'intero codice genetico. Anche la forma di certi organismi può essere a spirale come quella dell'ammonite, vissuto 300.000.000 di anni fa.
Archimede ne scrisse un trattato, "Sulle Spirali". anche nella natura inanimata scopriamo spirali come ad esempio la galassia a spirale.
Le spirali sono anche alla base dei frattali. Ci sono tre tipi comuni di spirali piane, la più importante delle quali per quanto riguarda i frattali è la spirale logaritmica. La spirale evoluta è quella che si ottiene srotolando un gomitolo e tenendo il filo sempre teso; la fine del filo traccerà una spirale.
Il modo migliore per rappresentarla è con le coordinate polari r e f che costituiscono una valida alternativa alle coordinate cartesiane. r corrisponde alla distanza del punto P dall'origine (in modulo) e f all'angolo tra OP e l'asse delle x. Da notare che r è sempre maggiore o uguale a 0 e l'angolo cresce in senso antiorario da 0 e una rotazione completa aumenta l'angolo di 2p radianti.
La spirale di Archimede è la più semplice ed è espressa in coordinate polari con la formula r = af. Tutte le spirali di Archimede sono simili, differiscono solo per scala.
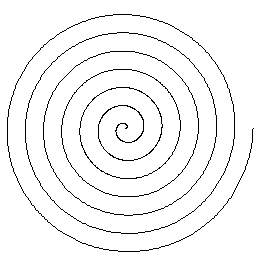
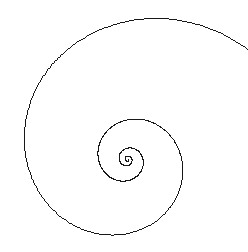
La spirale logaritmica sostituisce la r della spirale di Archimede con il
log r, log r = af. Se a è maggiore di 0 la
spirale cresce all'infinito, se è minore di 0 procede verso il centro, se
a=0 si ha una circonferenza. Il fattore di crescita dipende da
f. Si può interpretare come gli spostamenti di
una barca attorno ad un faro. Dopo un tratto in linea retta con angolo
iniziale b rispetto alla linea che la congiunge
con il faro, la nave avrà un angolo di b + a e
dovrà aggiustare la rotta. Considerando spostamenti infinitesimi, riducendo
a, si arriva ad una spirale indistinguibile da
una spirale matematica.
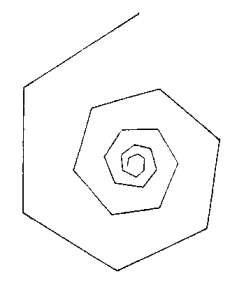
Nel 1957 A. E. Bosman con La geometria nel pianeta: un campo miracoloso
di ricerca voleva mostrare le miracolose figure geometriche della
natura, prima fra tutte la spirale. Una delle sue figure più importanti è
l'albero di Pitagora la cui costruzione è basata sul sistema binario.
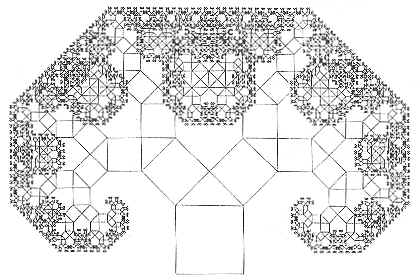
Un quadrato ha un lato in comune con un triangolo rettangolo isoscele, che
a sua volta ha gli altri due lati in comune con altri due quadrati e così
via. La somma delle aree dei due quadrati più piccoli, per il teorema di
Pitagora, è uguale all'area del quadrato iniziale e così anche le aree dei
quadrati che si formano nei passaggi successivi, sommate, daranno l'area
del primo quadrato. Si può avere un albero asimmetrico semplicemente
costruendo un triangolo rettangolo qualsiasi sul lato del primo quadrato.
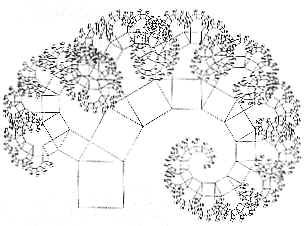
La forma avvolta non è altro che una spirale logaritmica.
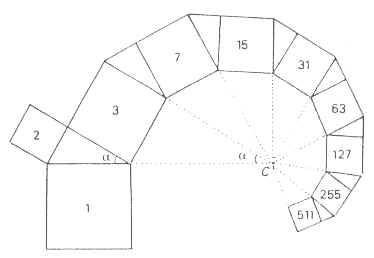
Si possono creare infinite spirali partendo dai quadrati.
L'albero di Pitagora è un buon esempio di frattale matematico. Vi sono
anche frattali a forma di stella, costruiti per esempio con una linea
chiusa e successivi segmenti che si incrociano tutti con lo stesso angolo.
Si può comparare la curva di von Koch con una costa della Bretagna, ma la natura è creata con casualità. Se si considera la somiglianza statisticamente si creano frattali più realistici. Per far ciò occorre che ogni parte del frattale abbia le stesse proprietà statistiche. I metodi basati sul caso sono detti metodi di Monte Carlo, e in modo più formale stocastici dal verbo greco che sta per indovinare.
Si può vedere come i frattali siano influenzati da una certa casualità controllata. Ci sono diversi modi di introdurre il caso nella costruzione dei frattali e oggi ci sono programmi per computer che possono creare lunghe serie arbitrarie di numeri casuali. Per esempio si sceglie un numero di 4 cifre e si eleva al quadrato, poi si tolgono la prima e l'ultima cifra finché non rimangono ancora 4 numeri, si procede ancora con il quadrato e con il taglio delle cifre e così via: il risultato è una serie di numeri casuali tra 0 e 9999 che non fallisce test statistici di casualità e nello stesso tempo e stata creata con una regola precisa.
Tutto deriva dal primo numero, quindi è una sequenza deterministica, ma dà l'impressione che sia caotica.
Un buon metodo molto pratico per i frattali basato sulla casualità è pensare al fatto che i frattali sono formati da un numero infinito di punti e che si può rappresentare solo una frazione di essi, un illusione della loro completezza. Analizzando ad esempio l'albero di Pitagora scopriamo che sono stati rappresentati solo i primi 12 passaggi. Introducendo una certa casualità nella costruzione si potrebbe stabilire di lasciare al caso la decisione di creare una spirale verso sinistra o verso destra a seconda della disposizione dei lati dei triangoli rettangoli. Questa introduzione di piccoli disturbi nella costruzione di frattali rende questi ultimi più simili a oggetti naturali come alberi, piante, coralli e spugne.
Si è sviluppata quindi una branca della geometria frattale che studia i cosiddetti frattali biomorfi, cioè simili ad oggetti presenti in natura. I risultati a volte sono stati stupefacenti. Uno dei frattali biomorfi più riusciti è la foglia di felce i cui dettagli, detti autosimili, riproducono sempre la stessa figura.
Si può comparare la curva di von Koch con una costa della Bretagna, ma la natura è creata con casualità. Se si considera la somiglianza statisticamente si creano frattali più realistici. Per far ciò occorre che ogni parte del frattale abbia le stesse proprietà statistiche. I metodi basati sul caso sono detti metodi di Monte Carlo, e in modo più formale stocastici dal verbo greco che sta per indovinare.
Si può vedere come i frattali siano influenzati da una certa casualità controllata. Ci sono diversi modi di introdurre il caso nella costruzione dei frattali e oggi ci sono programmi per computer che possono creare lunghe serie arbitrarie di numeri casuali. Per esempio si sceglie un numero di 4 cifre e si eleva al quadrato, poi si tolgono la prima e l'ultima cifra finché non rimangono ancora 4 numeri, si procede ancora con il quadrato e con il taglio delle cifre e così via: il risultato è una serie di numeri casuali tra 0 e 9999 che non fallisce test statistici di casualità e nello stesso tempo e stata creata con una regola precisa.
Tutto deriva dal primo numero, quindi è una sequenza deterministica, ma dà l'impressione che sia caotica.
Un buon metodo molto pratico per i frattali basato sulla casualità è pensare al fatto che i frattali sono formati da un numero infinito di punti e che si può rappresentare solo una frazione di essi, un illusione della loro completezza. Analizzando ad esempio l'albero di Pitagora scopriamo che sono stati rappresentati solo i primi 12 passaggi. Introducendo una certa casualità nella costruzione si potrebbe stabilire di lasciare al caso la decisione di creare una spirale verso sinistra o verso destra a seconda della disposizione dei lati dei triangoli rettangoli. Questa introduzione di piccoli disturbi nella costruzione di frattali rende questi ultimi più simili a oggetti naturali come alberi, piante, coralli e spugne.
Si è sviluppata quindi una branca della geometria frattale che studia i cosiddetti frattali biomorfi, cioè simili ad oggetti presenti in natura. I risultati a volte sono stati stupefacenti. Uno dei frattali biomorfi più riusciti è la foglia di felce i cui dettagli, detti autosimili, riproducono sempre la stessa figura.

Attraverso una semplice operazione, la biforcazione di un segmento, si
possono ottenere delle "fronde" molto realistiche.

E' interessante notare, parlando in termini informatici, che se si potesse
riuscire ad aumentare il livello di realismo, la quantità di informazioni
(quindi la dimensione di un file) da fornire al computer per visualizzare
una felce su schermo, sarebbe infinitamente minore. Questo uso della
geometria frattale è studiato da diversi anni e viene chiamato IFS
(Iterated Function System).
Robert Brown nel 1828 scoprì che le particelle al microscopio si muovevano in modo imprevedibile e casuale. Questo è stato chiamato moto browniano. L'idea della curva di un frattale può aiutare a farsi un'impressione della traiettoria di un moto browniano. Si deduce che le proprietà statistiche non variano a seconda della scala. I frattali browniani sono molto naturali. Un paesaggio lunare potrebbe apparire come la superficie di un frattale: il crateri più grandi rappresentano la scala maggiore, ma anche con qualsiasi scala minore si possono vedere crateri; la locazione dei quali è del tutto casuale.
Robert Brown nel 1828 scoprì che le particelle al microscopio si muovevano in modo imprevedibile e casuale. Questo è stato chiamato moto browniano. L'idea della curva di un frattale può aiutare a farsi un'impressione della traiettoria di un moto browniano. Si deduce che le proprietà statistiche non variano a seconda della scala. I frattali browniani sono molto naturali. Un paesaggio lunare potrebbe apparire come la superficie di un frattale: il crateri più grandi rappresentano la scala maggiore, ma anche con qualsiasi scala minore si possono vedere crateri; la locazione dei quali è del tutto casuale.

Cenni storici e teorie.
Matematica dei frattali.
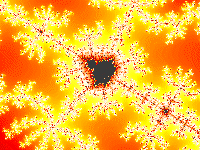
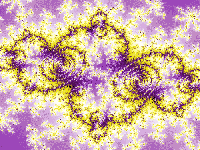
I frattali sono figure geometriche caratterizzate dal ripetersi sino all'infinito di uno stesso motivo su scala sempre più ridotta. Questa è la definizione più intuitiva che si possa dare di figure che in natura si presentano con una frequenza impressionante ma che non hanno ancora una definizione matematica precisa: l'atteggiamento corrente è quello di considerare frattale un insieme F che abbia proprietà simili alle quattro elencate qui di seguito:
1) Autosimilarità: F è unione di un numero di parti che, ingrandite di un certo fattore, riproducono tutto F; in altri termini F è unione di copie di se stesso a scale differenti.

|
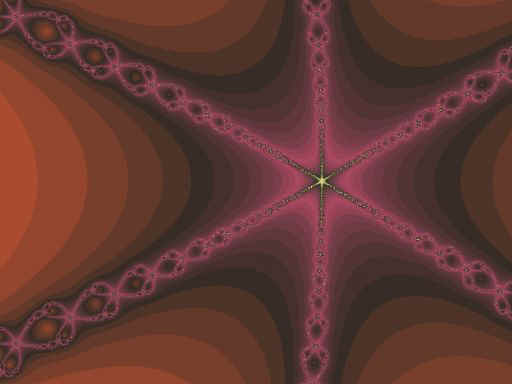
|
2) Struttura fine: F rivela dettagli ad ogni ingrandimento.
|

|
|

|

|
|
3) Irregolarità: F non si può descrivere come luogo di punti che
soddisfano semplici condizioni geometriche o analitiche. (la funzione è
ricorsiva: F = {Z | Z = f(f(f(...)))}
4) Dimensioni di autosimilarità > della dimensione topologica
La caratteristica di queste figure, caratteristica dalla quale deriva il loro nome, è che, sebbene esse possano essere rappresentate (se non si pretende di rappresentare infinite iterazioni, cioè trasformazioni per le quali si conserva il particolare motivo geometrico) in uno spazio convenzionale a due o tre dimensioni, la loro dimensione non è intera. In effetti la lunghezza di un frattale "piano" non può essere misurata definitamene, ma dipende strettamente dal numero di iterazioni al quale si sottopone la figura iniziale.
Fino agli inizi di questo secolo la geometria ha considerato oggetti per la cui trattazione è sufficiente la definizione classica e intuitiva di dimensione (Dt = dimensione topologica), già presente almeno implicitamente in Euclide. In questa definizione, data compiutamente da Poincaré, si assegna ad un punto o a un insieme totalmente sconnesso di punti Dt = 0; per le rette, induttivamente, la Dt = 1 in quanto possono essere divise da elementi di Dt = 0 (o meglio, un insieme F ha dimensione 1 se ogni punto ha un intorno in F arbitrariamente piccolo con frontiera di dimensione zero); e in generale un oggetto si dice di dimensione Dt = Dt'; quando ogni punto dell'insieme ha un intorno in F con frontiera di dimensione Dt = (Dt'-1). La dimensione topologica è un numero intero.
Il concetto di dimensione ha però diverse connotazioni matematiche, in accordo con le seguenti proprietà:
Siano A e B insiemi di punti:
Per l'insieme di Cantor, si ha Dt(C) = 0. Tale definizione non distingue tra C e l'insieme dei razionali nell'intervallo [0,1]. Per questo B. B. Mandelbrot, autorevole matematico che ha dato l'impulso allo studio dei frattali, evidenziò come la dimensione topologica non sia opportuna per le figure frattali, e per questo nello studiare queste figure si fa riferimento alla definizione di dimensione data da Kolmogorov-Hausdorff.
Si misuri un insieme di punti A con un'unità di misura h ogni volta più piccola e si chiami N(h) il minimo numero di segmenti (se il frattale è costituito da punti appartenenti ad una stessa retta) - o in generale di figure a k dimensioni se il frattale è costituito da punti tutti appartenenti ad uno spazio Âk - necessari per coprire per intero la figura, si definisce capacità di A:
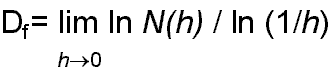
Analizziamo ora la dimensione del frattale più classico e studiato: l'insieme C di Cantor.
4) Dimensioni di autosimilarità > della dimensione topologica
La caratteristica di queste figure, caratteristica dalla quale deriva il loro nome, è che, sebbene esse possano essere rappresentate (se non si pretende di rappresentare infinite iterazioni, cioè trasformazioni per le quali si conserva il particolare motivo geometrico) in uno spazio convenzionale a due o tre dimensioni, la loro dimensione non è intera. In effetti la lunghezza di un frattale "piano" non può essere misurata definitamene, ma dipende strettamente dal numero di iterazioni al quale si sottopone la figura iniziale.
Fino agli inizi di questo secolo la geometria ha considerato oggetti per la cui trattazione è sufficiente la definizione classica e intuitiva di dimensione (Dt = dimensione topologica), già presente almeno implicitamente in Euclide. In questa definizione, data compiutamente da Poincaré, si assegna ad un punto o a un insieme totalmente sconnesso di punti Dt = 0; per le rette, induttivamente, la Dt = 1 in quanto possono essere divise da elementi di Dt = 0 (o meglio, un insieme F ha dimensione 1 se ogni punto ha un intorno in F arbitrariamente piccolo con frontiera di dimensione zero); e in generale un oggetto si dice di dimensione Dt = Dt'; quando ogni punto dell'insieme ha un intorno in F con frontiera di dimensione Dt = (Dt'-1). La dimensione topologica è un numero intero.
Il concetto di dimensione ha però diverse connotazioni matematiche, in accordo con le seguenti proprietà:
Siano A e B insiemi di punti:
- A = Âk Þ dim(A) = k
- AÍB Þ dim(A) £ dim(B)
- A Í Âk (A è aperto) Þ dim(A) = k
- A numerabileÞ dim(A) = 0
- dim(A) non varia se A è sottoposto a rotazioni, traslazioni, cambiamenti di scala (autosimilarità)
- dim(A È B) = max{ dim(A), dim(B) }
Per l'insieme di Cantor, si ha Dt(C) = 0. Tale definizione non distingue tra C e l'insieme dei razionali nell'intervallo [0,1]. Per questo B. B. Mandelbrot, autorevole matematico che ha dato l'impulso allo studio dei frattali, evidenziò come la dimensione topologica non sia opportuna per le figure frattali, e per questo nello studiare queste figure si fa riferimento alla definizione di dimensione data da Kolmogorov-Hausdorff.
Si misuri un insieme di punti A con un'unità di misura h ogni volta più piccola e si chiami N(h) il minimo numero di segmenti (se il frattale è costituito da punti appartenenti ad una stessa retta) - o in generale di figure a k dimensioni se il frattale è costituito da punti tutti appartenenti ad uno spazio Âk - necessari per coprire per intero la figura, si definisce capacità di A:
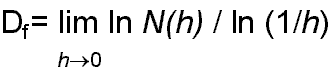
Analizziamo ora la dimensione del frattale più classico e studiato: l'insieme C di Cantor.

Questo insieme è costituito dai punti che "rimangono" sul segmento [0, 1] dopo che da questo è stato asportato (prima iterazione, p = 1) il terzo centrale (1/3, 2/3), e da ognuno dei due segmenti risultanti [0, 1/3] e [2/3, 1] è stato asportato il terzo centrale, esclusi gli estremi, e così via per infinite iterazioni. Evidentemente per p ® ¥ l'insieme C è costituito dagli estremi dei segmenti che si formano ad ogni iterazione, quindi è costituito da infiniti punti. La lunghezza dei segmenti asportati, dopo la p-esima iterazione, è data dall'espressione
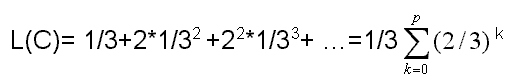
che è ovviamente uguale a 1 per p® ¥.
Si dimostra così che la lunghezza complessiva dell'insieme di Cantor è zero, e altresì che è costituito da infiniti punti. Quindi la definizione classica di dimensione è assolutamente inefficace.
Nel 1941, cioè prima che fosse data la definizione di Kolmogorov (1958), Courant e Robbins, forse non abituati né pronti all'idea di dimensione non intera, scrissero che la dimensione di C era zero. Evidentemente essi calcolarono solo la Dt, senza rendersi conto che questa è un dato sterile, che non permette di operare con questi insoliti oggetti matematici.
Oggi calcoliamo invece Df(C) prendendo inizialmente un segmento unitario, che, essendo della stessa lunghezza del segmento di partenza, lo copre al meglio; dopo la p = 1, i due segmenti rimanenti sono "misurati" da N(h) = 2 segmenti di h = 1/3; in generale, dopo p iterazioni, N(h) = 2p e h = 3-p. Da questo si ricava che
Df(C) = ln 2p / ln 1/3 -p = ln 2 / ln 3 » 0,6309...
Il fatto che la dimensione di C sia 0 < Df(C) < 1, fa immediatamente capire come l'insieme C non contenga segmenti continui, ma sia costituito da infiniti punti, che sono tutti di accumulazione per C stesso, infatti in ogni intorno U(x Î C, e) esistono infiniti punti derivanti dalle iterazioni successive, e quindi C è un insieme perfetto perchè non ci sono punti di accumulazione di C che non appartengano a C stesso (tutti gli estremi dei segmenti appartengono a C).
E' interessante osservare che questi infiniti punti hanno la potenza del continuo! Infatti a ogni numero x Î [0, 1], si può associare la rappresentazione ternaria della misura della distanza dallo zero, e si può scrivere nella forma: x = 0,a1a2...an, dove ai = 0 oppure 1 oppure 2. Tale rappresentazione non è unica: per esempio 1/3 = 0,1(0) ma anche 1/3 = 0,0(2); in simili casi decidiamo di scegliere la rappresentazione che contiene meno cifre "1"; in tal modo, ogni numero è rappresentato in modo univoco. Si può dimostrare che x appartiene all'insieme di Cantor se e solo se la sua rappresentazione (in base 3) non contiene la cifra 1.
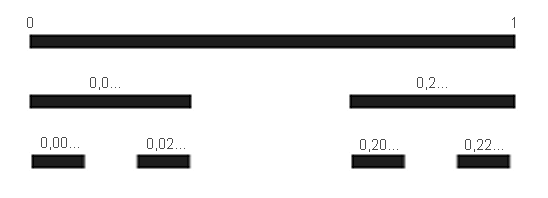
Si osservi ora che le rappresentazioni composte con le cifre 0 e 2 sono
tante quante quelle composte con le cifre 0 e 1 e di queste ultime ve ne è
una infinità continua (cioè con la potenza del continuo), poichè ogni
numero dell'intervallo [0, 1] si può rappresentare con una tale successione
usando il sistema binario. In conclusione i punti di Cantor sono
un'infinità continua.
Inoltre, un aspetto interessante della matematica dei frattali è l'utilizzo di una numerazione in basi diverse da quella decimale in relazione alle caratteristiche del singolo motivo geometrico. Questo procedimento è utile soprattutto per l'elaborazione da parte di computer, che non sono legati a nessuna base (diversa da quella binaria) più che a quella decimale. In questo modo, per esempio, prendendo un segmento unitario e utilizzando la base 3, l'insieme di Cantor è semplicemente costituito da tutti quei punti xn per i quali la misura della distanza d(xn) dall'estremo che noi chiameremo zero (o origine del segmento) è espressa come una successione infinita di cifre ternarie 0,a1a2...an, dove il valore delle ai sia solamente zero o due. Infatti riscontriamo che, dopo la prima iterazione, i punti del primo terzo hanno 0 £ d(xprimo terzo) £ 0,1 e che i punti del terzo di segmento adiacente al secondo estremo hanno 0,2 £ d(xultimo terzo) £ 1. Per la proprietà di autosimilarità, questo ragionamento può essere esteso alla seconda iterazione, considerando la seconda cifra dello sviluppo ternario della misura della d(x) dei punti che appartengono all'insieme dopo la p = 1. Facilmente si capisce come anche il punto x | d(x) = 0,1 appartenga all'insieme, scegliendo opportunamente la rappresentazione di 0,1 = 0,0(2).
Altri frattali vengono creati da computer attraverso l'uso di basi numeriche non decimali. Consideriamo per esempio la curva di Von Koch, nata come esempio di curva priva di tangente in alcun punto.
Inoltre, un aspetto interessante della matematica dei frattali è l'utilizzo di una numerazione in basi diverse da quella decimale in relazione alle caratteristiche del singolo motivo geometrico. Questo procedimento è utile soprattutto per l'elaborazione da parte di computer, che non sono legati a nessuna base (diversa da quella binaria) più che a quella decimale. In questo modo, per esempio, prendendo un segmento unitario e utilizzando la base 3, l'insieme di Cantor è semplicemente costituito da tutti quei punti xn per i quali la misura della distanza d(xn) dall'estremo che noi chiameremo zero (o origine del segmento) è espressa come una successione infinita di cifre ternarie 0,a1a2...an, dove il valore delle ai sia solamente zero o due. Infatti riscontriamo che, dopo la prima iterazione, i punti del primo terzo hanno 0 £ d(xprimo terzo) £ 0,1 e che i punti del terzo di segmento adiacente al secondo estremo hanno 0,2 £ d(xultimo terzo) £ 1. Per la proprietà di autosimilarità, questo ragionamento può essere esteso alla seconda iterazione, considerando la seconda cifra dello sviluppo ternario della misura della d(x) dei punti che appartengono all'insieme dopo la p = 1. Facilmente si capisce come anche il punto x | d(x) = 0,1 appartenga all'insieme, scegliendo opportunamente la rappresentazione di 0,1 = 0,0(2).
Altri frattali vengono creati da computer attraverso l'uso di basi numeriche non decimali. Consideriamo per esempio la curva di Von Koch, nata come esempio di curva priva di tangente in alcun punto.
 p = 1
p = 1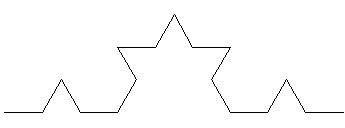 p = 2
p = 2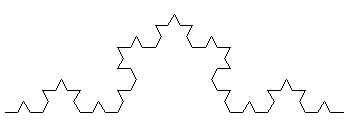 p = 3
p = 3
Per questa curva Df(K) = ln 4 / ln 3, per p
® ¥, mentre la sua lunghezza è evidentemente
(4/3)p, cioè infinita: per disegnare perfettamente questa curva,
anche supponendo di poterlo fare alla velocità della luce, sarebbe
necessario un tempo infinito. Se prendiamo due punti appartenenti a K, con
distanza euclidea e comunque piccola, la
lunghezza della curva che porta dal primo al secondo (e viceversa) è
infinita. Inoltre, se costruissimo una curva di Koch su ogni lato di un
triangolo equilatero, la lunghezza del perimetro della figura così ottenuta
sarebbe infinita come già visto, mentre la sua area, posta l'area iniziale
del triangolo Ai = a,
 .
.
Ora abbandoniamo i frattali "semplici", generati cioè da successive trasformazioni geometriche e consideriamo invece frattali F costituiti dai punti che soddisfano una funzione complessa  2 (anche se, teoricamente, non c'è un limite alla dimensione topologica di un frattale, per comodità di rappresentazione noi studieremo solo frattali Julia e Mandelbrot, che si rappresentano nel piano di Argand-Gauss, facendo quindi uso della matematica complessa) del tipo Z = f(z), dove zp = Zp-1, cioè una funzione nella quale per ogni iterazione, z assume il valore di Z ottenuto nell'iterazione precedente.
In altre parole, F = { Z | Z = f(f(f(f(...)))) }
E' proprio questo che genera l'indefinitezza che è una delle caratteristiche peculiari di tali costruzioni matematiche, ovvero la possibilità di iterare virtualmente all'infinito per ciascun punto prima di passare al successivo. Quindi, per "disegnare" un frattale attraverso un elaboratore, è necessario precisare il numero massimo di iterazioni: un tempo finito non basterebbe per calcolare un punto del frattale a infinite iterazioni.
Volendo essere un po' più precisi, si può dire che un frattale non rappresenta altro che la "forma" del bacino di attrazione di una successione a valori complessi definita per ricorrenza, rappresentata sul piano di Argand-Gauss.
Utilizzando la funzione f(z): Z = z2 + c si ottengono i due tipi di frattali che noi studieremo principalmente: i famosi "Julia" e "Mandelbrot" (che sono generati dalla stessa equazione, ma con valori differenti per il parametro c).
L'equazione è quella che nella rappresentazione abituale genera una parabola (se z Î Â) traslata col vertice in (0, c); quello che interessa a noi, tuttavia, non è la solita rappresentazione sul piano cartesiano (ovvero secondo un incremento della variabile indipendente), ma come si comporta, dato un punto di partenza, reimpostando nell'equazione i risultati dell'elaborazione precedente (zp = Zp-1).
Con l'aiuto dei calcolatori e utilizzando opportunamente i colori è possibile ottenere immagini molto suggestive di questi frattali.
Dalla determinazione delle condizioni di partenza, dipendono le differenze tra gli insiemi di Julia e l'insieme di Mandelbrot. E' necessario un esempio, perchè gran parte della difficoltà iniziale che si incontra avvicinandosi ai frattali sta in questo.
 .
.
Ora abbandoniamo i frattali "semplici", generati cioè da successive trasformazioni geometriche e consideriamo invece frattali F costituiti dai punti che soddisfano una funzione complessa  2 (anche se, teoricamente, non c'è un limite alla dimensione topologica di un frattale, per comodità di rappresentazione noi studieremo solo frattali Julia e Mandelbrot, che si rappresentano nel piano di Argand-Gauss, facendo quindi uso della matematica complessa) del tipo Z = f(z), dove zp = Zp-1, cioè una funzione nella quale per ogni iterazione, z assume il valore di Z ottenuto nell'iterazione precedente.
In altre parole, F = { Z | Z = f(f(f(f(...)))) }
E' proprio questo che genera l'indefinitezza che è una delle caratteristiche peculiari di tali costruzioni matematiche, ovvero la possibilità di iterare virtualmente all'infinito per ciascun punto prima di passare al successivo. Quindi, per "disegnare" un frattale attraverso un elaboratore, è necessario precisare il numero massimo di iterazioni: un tempo finito non basterebbe per calcolare un punto del frattale a infinite iterazioni.
Volendo essere un po' più precisi, si può dire che un frattale non rappresenta altro che la "forma" del bacino di attrazione di una successione a valori complessi definita per ricorrenza, rappresentata sul piano di Argand-Gauss.
Utilizzando la funzione f(z): Z = z2 + c si ottengono i due tipi di frattali che noi studieremo principalmente: i famosi "Julia" e "Mandelbrot" (che sono generati dalla stessa equazione, ma con valori differenti per il parametro c).
L'equazione è quella che nella rappresentazione abituale genera una parabola (se z Î Â) traslata col vertice in (0, c); quello che interessa a noi, tuttavia, non è la solita rappresentazione sul piano cartesiano (ovvero secondo un incremento della variabile indipendente), ma come si comporta, dato un punto di partenza, reimpostando nell'equazione i risultati dell'elaborazione precedente (zp = Zp-1).
Con l'aiuto dei calcolatori e utilizzando opportunamente i colori è possibile ottenere immagini molto suggestive di questi frattali.
Dalla determinazione delle condizioni di partenza, dipendono le differenze tra gli insiemi di Julia e l'insieme di Mandelbrot. E' necessario un esempio, perchè gran parte della difficoltà iniziale che si incontra avvicinandosi ai frattali sta in questo.
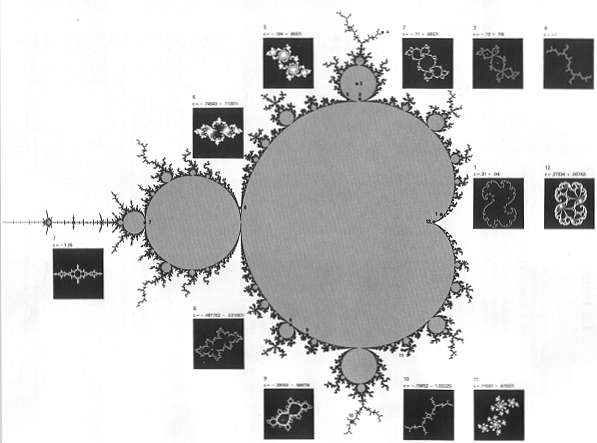
L'insieme di Mandelbrot si presenta come un otto disposto in orizzontale
sfrangiato e simmetrico rispetto all'asse delle ascisse.
Possiamo adesso entrare un poco più in dettaglio ed affrontare i principi di determinazione dei frattali della famiglia di Julia, che si presentano molto diversamente a seconda della scelta del termine noto c.
N. B. Il numero di iterazioni massime determina la precisione da adottare per la rappresentazione dell'insieme e per ottenere migliori risultati, è consigliabile che sia uguale o comunque inferiore al numero di colori disponibili.
Buoni risultati si ottengono assegnando a c dei coefficenti reali ed immaginari compresi fra 0 ed 1.
Vi sono infiniti insiemi di Julia poichè la scelta di c non deve sottostare a nessuna restrizione.
La differenza fra l'insieme di Mandelbrot e gli insiemi di Julia è che le coordinate complesse del punto del piano vengono sostituite non a z, inizialmente azzerato, ma a c, che non è più una costante definita all'inizio dell'elaborazione.
Questa immagine mostra l'insieme di Mandelbrot ottenuta con un numero crescente di iterazioni massime: come si può notare, la precisione del disegno dei confini diventa sempre più accurata.
- Si supponga di considerare una piccola porzione attorno all'origine di un piano complesso di intervallo (-2, -2) - (2, 2).
- Si sostituiscano, per ogni punto considerato, le corrispondenti coordinate complesse al termine noto c, nell'equazione Z = z2 + c, ponendo inizialmente z = 0 + 0i.
- Si calcoli il valore di Z.
- Se si trova che la distanza di Z dall'origine è maggiore di due, si salti al passo 6. Per calcolare tale distanza, si adotta il teorema di pitagora nel seguente modo: dato Z = a + bi, il quadrato della distanza d dall'origine sarà d2 = a2 + b2.
- Se no, si incrementi di 1 un contatore e si torni al passo 3 se il contatore ha un valore inferiore al numero di iterazioni massime prefissato, dopo aver posto z = Z.
- Si colori il punto di un colore diverso a seconda del valore del contatore.
- Si azzeri il contatore e si ritorni al passo 2, per calcolare il colore del prossimo punto.
- Il procedimento avrà termine quando tutti i punti interessati saranno stati processati nel suddetto modo.
Possiamo adesso entrare un poco più in dettaglio ed affrontare i principi di determinazione dei frattali della famiglia di Julia, che si presentano molto diversamente a seconda della scelta del termine noto c.
- Si supponga considerare una piccola porzione attorno all'origine di un piano complesso di intervallo (-2, -2) - (2, 2).
- Si scelga un binomio complesso c assegnando valori del tutto arbitrari alla parte reale ad alla parte immaginaria.
- Si sostituiscano, per ogni punto considerato, le corrispondenti coordinate complesse alla variabile z, nell'equazione Z = z2 + c.
- Si calcoli il valore di Z.
- Se si trova che la distanza di Z dall'origine è maggiore di due, si salti al passo 7. Per calcolare tale distanza, si adotta il teorema di Pitagora come spiegato sopra.
- Se no, si incrementi di 1 un contatore e si torni al passo 4 se il contatore ha un valore inferiore al numero di iterazioni massime prefissato, dopo aver posto z = Z.
- Si colori il punto di un colore diverso a seconda del valore del contatore.
- Si azzeri il contatore e si ritorni al passo 3 per calcolare il colore del prossimo punto.
- Il procedimento avrà termine quando tutti i punti interessati saranno stati processati nel suddetto modo.
N. B. Il numero di iterazioni massime determina la precisione da adottare per la rappresentazione dell'insieme e per ottenere migliori risultati, è consigliabile che sia uguale o comunque inferiore al numero di colori disponibili.
Buoni risultati si ottengono assegnando a c dei coefficenti reali ed immaginari compresi fra 0 ed 1.
Vi sono infiniti insiemi di Julia poichè la scelta di c non deve sottostare a nessuna restrizione.
La differenza fra l'insieme di Mandelbrot e gli insiemi di Julia è che le coordinate complesse del punto del piano vengono sostituite non a z, inizialmente azzerato, ma a c, che non è più una costante definita all'inizio dell'elaborazione.
Questa immagine mostra l'insieme di Mandelbrot ottenuta con un numero crescente di iterazioni massime: come si può notare, la precisione del disegno dei confini diventa sempre più accurata.


Best fractals zoom ever
RispondiEliminawww.youtube.com
BELLISSIMO!!! Grazie per la condivisione!!!!
RispondiElimina^_^
bellissima spiegazione e nuova visione del Cosmo. Purtroppo sono 800 anni che ci tengono nascosto i numeri di Fibonacci e i frattali,ma di cosa hanno paura di scoprire la verità
RispondiEliminaFreedomPop is Britian's #1 COMPLETELY FREE mobile phone provider.
RispondiEliminaWith voice, SMS & data plans are priced at £0.00/month.
Order a professional Sparkling White Smiles Custom Teeth Whitening System online and enjoy BIG SAVINGS!
RispondiElimina* 10 shades whiter in days!
* Results Are Guaranteed.
* As good as your dentist.
* Same strength Teeth Whitening Gel as dentists use.
Are you looking for free YouTube Views?
RispondiEliminaDid you know that you can get them AUTOMATICALLY AND ABSOLUTELY FREE by registering on Like 4 Like?