parte 1.1
parte 1.2
Luce e fenomeni elettromagnetici: gli Egizi già lo sapevano?
James Clerk Maxwell.
parte 2.1
parte 2.2
La grande sintesi di Maxwell.
Alcune importanti nozioni di elettromagnetismo. I principi fondamentali di questa vasta teoria furono stabiliti nel corso del secolo XIX dai fondamentali lavori di Charles-Augustin de Coulomb (1736-1806), Hans Christian Oersted (1777-1851), André-Marie Ampère (1775-1836), Joseph Henry (1797-1878) e soprattutto di Michael Faraday (1791-1867). I loro risultati furono poi sintetizzati da Carl Fredrich Gauss (1777-1855) nei seguenti due teoremi, che stabiliscono i primi due principi fondamentali dell'elettromagnetismo:
1)
Un
corpo carico produce nello spazio circostante delle linee di forza elettriche,
il cui flusso attraverso una superficie chiusa è pari alla somma delle cariche
poste al suo interno divisa per la costante dielettrica.
2)
Una corrente elettrica che circola in un conduttore
produce delle linee di forza magnetiche attorno al conduttore, il cui
flusso
attraverso una superficie chiusa è sempre nullo.
La
prima affermazione è detta Teorema
di Gauss del campo elettrico, e matematicamente si può scrivere così:
mentre
la seconda viene detta anche Teorema di Gauss del campo
magnetico:
dove
la lettera greca Φ
indica il flusso attraverso la superficie S.
Il
primo teorema ha il seguente significato fisico: esiste il monopolo
elettrico,
cioè la carica elettrica singola, ed essa è sorgente di campo
elettrico. Il secondo teorema ci dice
invece che il campo magnetico è solenoidale, ovvero che le linee di forza sono
sempre chiuse, e NON esiste il monopolo magnetico. Spezzando un magnete in due,
infatti, trovo sempre due magneti dotati entrambi di polo Nord e polo Sud.
E'
a questo punto che fa irruzione nella storia della scienza il grande fisico e
matematico scozzese James
Clerk Maxwell (1831-1879). Negli anni tra il 1860 ed il 1870 egli sviluppò una teoria
matematica dell'elettromagnetismo nella quale partì dai due teoremi suddetti, oggi
noti come PRIMA e SECONDA EQUAZIONE DI MAXWELL. Egli
propose un modello onnicomprensivo per visualizzare le
relazioni esistenti tra le grandezze elettriche e magnetiche osservate
sperimentalmente da Faraday e soci. Egli lo descrisse matematicamente attraverso un sistema di equazioni,
oggi note
come equazioni di Maxwell, dalle quali si possono ottenere tutte le proprietà
dei campi elettrici e magnetici. Il
lavoro di Maxwell contiene alcune idee completamente nuove e ricche di conseguenze:
a)
un campo elettrico variabile nel tempo genera un campo magnetico.
b)
non solo le correnti nei conduttori producono dei campi attorno ad essi, ma
anche i campi elettrici variabili nel vuoto producono dei campi magnetici.
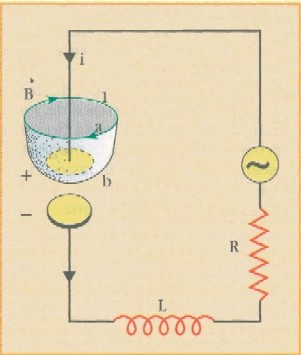 Il genio di Edimburgo
ragionò come segue.
Sia un circuito contenente un condensatore, come quello illustrato nella figura
a fianco; in regime di
corrente continua, il circuito risulta ovviamente aperto, cioè non passa alcuna
carica elettrica, e la circuitazione del campo elettrico calcolata lungo il
percorso chiuso 1 è nulla sia prendendo in considerazione la superficie piana
a
che quella curva b, essendo nulla la corrente concatenata con le due superfici,
cioè la corrente che le "buca" entrambe.
Il genio di Edimburgo
ragionò come segue.
Sia un circuito contenente un condensatore, come quello illustrato nella figura
a fianco; in regime di
corrente continua, il circuito risulta ovviamente aperto, cioè non passa alcuna
carica elettrica, e la circuitazione del campo elettrico calcolata lungo il
percorso chiuso 1 è nulla sia prendendo in considerazione la superficie piana
a
che quella curva b, essendo nulla la corrente concatenata con le due superfici,
cioè la corrente che le "buca" entrambe.
Diverso
è il discorso se la corrente i è
variabile nel tempo. Infatti in questo caso il
circuito dotato di condensatore non è chiuso, e la
circuitazione del campo B lungo la linea
l è pari, per il
teorema della
circuitazione di Ampére, al prodotto della corrente i per la permeabilità
magnetica del vuoto µ0. Allora, tale circuitazione è pari a zero se
si prende in considerazione la superficie b passante fra le armature del
condensatore, non "bucata" da alcuna corrente di conduzione, ed è
invece pari a µ0
i se si prende in considerazione la superficie
a.
Questo paradosso può essere risolto solo ammettendo l'esistenza, nello spazio
vuoto tra le due armature, di una corrente che non è di conduzione, non
essendoci cariche da spostare materialmente, ma che agli effetti del teorema
della circuitazione di Ampére è equivalente ad una corrente di conduzione.
Maxwell identificò tale corrente con quella
che egli chiamò corrente di spostamento.
Siccome essa dipende
dalla rapidità con cui varia la posizione delle cariche, egli concluse che essa deve
essere direttamente proporzionale alla rapidità con la quale varia nel tempo il flusso
del campo elettrico attraverso una superficie che ha come contorno il percorso l. E così il
grande fisico-matematico attribuì ad essa la seguente espressione:
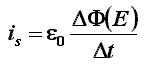
Di
conseguenza la legge di Ampére sull'induzione magnetica, fino ad ora
scritta nella forma C(B) = µ0 i, deve essere così modificata:
perché
alla corrente di conduzione i va aggiunta quella di spostamento
is.
Questa
non viene più attribuita al solo André-Marie
Ampére ma, giustamente, è detta
equazione di Ampére-Maxwell. e costituisce la TERZA
EQUAZIONE DI MAXWELL.
Certamente
questa ipotesi potrà apparire come un escamotage matematico volto a
salvaguardare la veridicità del teorema di Ampére; la corrente è sempre stata
intesa come un moto di cariche elettriche, siano essi elettroni (nei
conduttori), ioni positivi e negativi (nelle soluzioni e nei gas), elettroni e
lacune (nei semiconduttori); non si capisce dunque, a prima vista, come la
formula che esprime is possa essere definita una
corrente. Ad un esame più approfondito, invece, emerge il profondo significato
fisico dell'ipotesi di Maxwell: essa ci dice che il campo magnetico che
circonda la corrente di spostamento può essere considerato una conseguenza
della variazione nel tempo del campo elettrico.
Secondo
la teoria elaborata da Maxwell, insomma, i due principi fondamentali dell'elettromagnetismo,
che abbiamo già ricordato poco sopra e che erano già
stati stabiliti da altri scienziati, dovevano essere integrati da un terzo:
3)
un campo elettrico variabile nello spazio produce un campo magnetico.
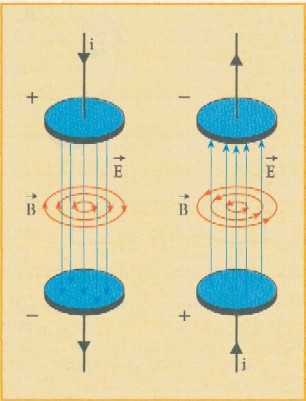 Il
vettore B del campo magnetico indotto sta in un piano perpendicolare al vettore
E del campo elettrico variabile e l'intensità di B dipende dalla rapidità con
cui varia E.
Il
vettore B del campo magnetico indotto sta in un piano perpendicolare al vettore
E del campo elettrico variabile e l'intensità di B dipende dalla rapidità con
cui varia E.
Consideriamo
dunque una coppia di conduttori piani collegati a un generatore di corrente,
come nella figura a sinistra. Mentre le cariche si avvicinano o si allontanano
dai piatti attraverso i conduttori collegati alla corrente, l'intensità E
del
campo elettrico nello spazio tra i piatti varia nel tempo. Come si è già
visto, questo campo elettrico variabile produce un campo magnetico nel
quale
l'intensità del vettore in un dato istante varia con la distanza dai
piatti. Cambiando segno alla carica sulle armature, e quindi il verso
del campo elettrico da a) a b), anche le linee di forza del campo
magnetico
indotto cambiano verso. Questo è il significato fisico della Terza
Equazione di
Maxwell.
Un'altra
proprietà dei campi elettrici e magnetici, già nota prima di Maxwell, acquista
un nuovo significato alla luce del suo lavoro, poiché risulta simmetrica alla
formulazione, enunciata poc'anzi, del terzo principio:
4)
un campo magnetico variabile nello spazio produce un campo elettrico.
Questo fenomeno di
induzione elettromagnetica era stato scoperto sperimentalmente (manco a dirlo!)
da Henry e dal solito Faraday, ed infatti la legge matematica
che la esprime è nota come equazione di Faraday-Henry:
Essa
significa che la circuitazione del campo elettrico indotto dal campo magnetico
variabile nel tempo è pari alla variazione nel tempo del flusso di tale campo
magnetico induttore. Il segno meno indica che la corrente indotta ha segno
opposto alla variazione di flusso che la produce, ed è nota come legge
di Lenz. Essa rappresenta un caso particolare di una legge universale
assai più generale, nota come principio di Le Chatêllier
ed esprimibile in questi termini:
quando
un sistema fisico viene perturbato, esso evolve nella direzione che tende a
minimizzare la perturbazione avvenuta.
Infatti,
quando il flusso di B varia nel tempo, viene indotta una corrente elettrica che
a sua volta genera un campo magnetico, il cui flusso ( per colpa di quel segno
meno) varia in direzione opposta a quella del campo B esterno. In tal modo, se
quest'ultimo sta diminuendo la corrente indotta cerca di sostenerlo, mentre se
sta aumentarlo cerca di tamponarne la crescita. L'equazione di Faraday-Henry e
la legge di Lenz, prese assieme, costituiscono la QUARTA
EQUAZIONE DI MAXWELL.
A
partire dalle quattro equazioni di Maxwell (0.3)
+ (0.4)
+ (0.5)
+ (0.6), è possibile ricavare
in ogni punto il valore del campo elettrico e del campo magnetico, a patto di
conoscere:
i)
la distribuzione delle cariche nello spazio;
ii)
la distribuzione delle correnti nei mezzi materiali o nel vuoto.
L'insieme
completo di relazioni tra i campi elettrici e magnetici proposto da Maxwell non
fu subito direttamente verificabile. Egli, però, aveva previsto anche un
fenomeno del tutto nuovo, che avrebbe dovuto insorgere per effetto delle
reciproche interazioni tra campi elettrici e magnetici variabili. Per capire di
cosa si tratta, supponiamo
che in una certa regione di spazio ad un certo istante si determini una
variazione del campo elettrico, originato, per esempio, da un moto accelerato di
cariche elettriche. Nei punti immediatamente vicini si produce allora, per la
terza equazione di Maxwell, un campo magnetico anch'esso variabile nel tempo. La
variazione del campo magnetico, per la quarta equazione di Maxwell, origina nei
punti immediatamente vicini un campo elettrico anch'esso variabile, e così via.
Nasce in tal modo una perturbazione elettromagnetica
che si propaga nello spazio.
Il
fatto che una variazione del campo magnetico in un punto produce un campo
elettrico variabile era noto già prima di Maxwell, in quanto era previsto
dalla legge di Faraday-Henry; si pensava però che, allorché un campo
magnetico bruscamente diminuiva da un valore massimo a zero, altrettanto
doveva fare il campo elettrico e il tutto cessava dopo un piccolo intervallo
di tempo dall'istante in cui si era annullato il campo magnetico. La novità
prevista da Maxwell consiste nel fatto che il campo elettrico ed il campo magnetico generati dalla variazione nel tempo di uno dei due sono in grado di
autosostenersi,
cioè di propagarsi anche se la variazione iniziale che li ha prodotti è venuta meno!
Se
ne conclude che, da una brusca variazione di un campo elettrico o magnetico
nel tempo, ha origine la propagazione di un impulso elettromagnetico, cioè di
un'ONDA, chiamata per l'appunto onda elettromagnetica.
Il
valore della velocità di propagazione delle onde elettromagnetiche nel vuoto coincide con buona approssimazione con quello della velocità della luce, noto dalle
esperienze di Fizeau e Foucault. Questo fu un risultato clamoroso che mise in
evidenza lo straordinario potere unificante delle equazioni di Maxwell.
Egli,
avendo notato che le onde elettromagnetiche e la luce, oltre ad essere
caratterizzate entrambe da vibrazioni trasversali, si propagano con la stessa
velocità, avanzò l'ipotesi della natura elettromagnetica della luce, l'idea nacque osservando che la velocità delle
onde elettromagnetiche nel vuoto
Luce. Lunghezza d'onda e frequenza.
parte 3.1
Per approfondimenti sui colori vedere giugno 2012.
parte 3.2
Elettricità e magnetismo.
Per approfondimenti su Nikola Tesla vedere luglio 2012.

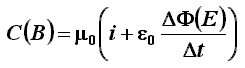
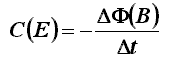
Nessun commento:
Posta un commento